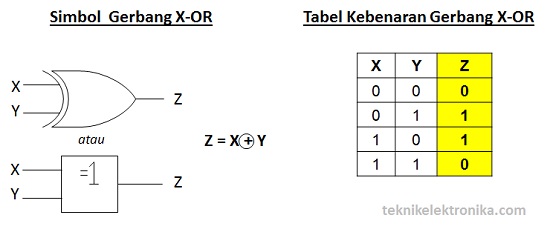
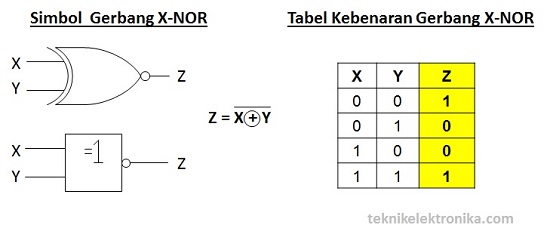
Integral Ganda
• Bentuk
I = Z Z f(x,y)dA
R
•
Arti geometri: volume daerah di bawah permukaan z = f(x,y) dengan alas R.
•
Perhitungan: menggunakan integral berulang
I = Z Z f(x,y)dxdy
R
atau
I = Z Z f(x,y)dydx
R
Urutan integral disesuaikan
dengan bentuk daerah R atau kemudahan
dalam perhitungan
Contoh:
Hitung RRR ey2dA dengan R daerah segitiga yang memiliki titik sudut (0,0), (1 , 1) dan
(0,1).
Jawab:
Penulisan
R = {(x,y) : 0 ≤ x ≤ y,0 ≤ y ≤ 1}
atau
R = {(x,y) : x ≤ y ≤ 1,0
≤ x ≤ 1}
Dari bentuk integran-nya ey2,
penggintegralan terhadap y lebih
dahulu tidak dimungkinkan, jadi
Perubahan variabel dalam integral
•
Bentuk RR e−(x2+y2)dA lebih
mudah dihitung menggunakan koordinat polar, dengan hubungan x = r
cosθ y = r sinθ
•
Secara umum perubahan koordinat:
Z Z f(x,y)dA
= Z
Z F(r,θ)rdrdθ
R R∗
dimana:
R∗daerah
integral dalam x − y
R daerah
integral dalam r − θ, sesuai transformasi yang berlaku F(r,θ)
= f(r cosθ,r sinθ) dA
dalam x − y menjadi rdrdθ
•
Integral di atas dengan R = {(x,y) : x2 + y2 ≤ a2}
dapat dinyatakan dalam polar
RR e−(x2+y2)dA = R2π R a e−r2−rdrdθ− 2
R 0 0
= ···
= π(1 e a )
dimana R∗ = {(r,θ) :
0 ≤ r ≤ a,0 ≤ θ ≤ 2π}
•
Bagaimana dengan bentuk y x
−
Z Z e y+xdA
y+xdA
R
dimana R = {(x,y) : 0 ≤ x ≤ 1 − y,0 ≤ y ≤ 1}.
Perlu transformasi dan
perumusan integral. Berikut kita bahas secara umum.
– Integral
I = Z Z F(x,y)dA
R
dengan transformasi (x,y) ↔ (u,v)
x = f(u,v) y = g(u,v)
secara geometri kita petakan u = konstan dan v = konstan ke kurvakurva pada bidang x − y.
– Luas daerah kecil dA, pada bidang x−y, hendak kita nyatakan dalam u dan v, diilustrasikan pada Gambar (1).
∗ Batas daerah dA:
-Lengkungan u dan u + du
-Lengkungan v dan v + dv
-Lengkungan v dan v + dv
Figure
1: Pemetaan kurva dari bidang x − y ke u
− v
∗ Perpotongan
lengkungan u dan lengkungan v berupa
r¯ = x¯i + y¯j
Di sini kita gunakan z = 0 karena lengkungan tersebut berada
di bidang x − y.
∗ Diferensial
dari r¯
∗ Vektor singgung pada v = konstan (dv = 0) adalah
dr¯|v=konstan
Hal serupa
untuk u = konstan (du = 0) berlaku
dr¯|u=konstan
Figure 2: Luas daerah sebagai
perkalian silang dari vektor singgung sepanjang lengkungan u konstan dan v konstan
∗ Luas sebagai perkalian silang
dua vektor singgung dari masing-masing lengkungan seperti diilustrasikan pada
Gambar (2).
Di sini digunakan dua pasangtanda tegak, yang pertama
(dalam) menyatakan determinan dan kedua (luar) menyatakan tanda mutlak. Penulisan
determinan pada baris terakhir dikenal sebagai determinan Jacobi, notasi
∗ Bentuk
integral
dimanamenyatakan daerah integral di
bidang u − v.
– Contoh semula:
−
Z Z ey y+xxdA
y+xxdA
R
dimana R = {(x,y) : 0 ≤ x ≤ 1 − y,0 ≤ y ≤ 1}.
Kita
gunakan u = y − x, v = y
+ x atau x = (v − u)/2,
y = (v + u)/2 ,
sehingga determinan Jacobi
Pemetaan
di atas dilakukan padabatas-batas daerah , menghasilkan
Figure
3: Pemetaan daerah integrasi dari R ke
D∗
sehingga
D∗ = {(u,v) : −v ≤ u ≤ v,0
≤ v ≤ 1}
seperti
diilustrasikan pada Gambar (3). Oleh karena itu integral dalam
u − v
Integral Garis
C kurva di
bidang dengan arah lintasan sesuai lintasan
C : r¯(t) = x(t)¯i
+ y(t)¯j, a ≤ t ≤ b
Di sini kurva diasumsikan mulus, yaitu kontinu sampai
turunan pertama. Selain itu, diberikan fungsi f(x,y) yang terdefini
pada kurva C dan kontinu. Integral
garis
Z f(x,y)ds
C
secara geometri
merupakan luas lempeng sepanjang lintasan C
yang tingginya
f(x,y)
dari dasar.
Masalah sekarang adalah bagaimana
menghitung integral tersebut. Secara fisis hal tersebut dapat dilakukan dengan
menarik lempeng yang berliku-liku menjadi terentang, sehingga permasalahan
menjadi integral tentu seperti pada kalkulus I (luas daerah di bawah kurva).
Proses merentang lempeng tersebut dapat diterjemahkan dalam matematika dengan
menyatakan integral yang dihadapi menjadi integral terhadap parameter t. Untuk itu, kita partisi selang [a,b], dan salah satunya [ti,ti+1], yang mempunyai panjang lintasan.
Sehingga integral garis dapat dinyatakan sebagai
C f(
x,y)
ds =
RRtt==ab f(
x(
t)
,y(
tq))
 dsdt′dt ′
dsdt′dt ′
= ab f(x(t),y(t)) x (t)2 + y (t)2dt
Contoh 1:
Hitung RC xy3ds dengan C : segmen garis y = 2x dari (-1,-2,0) ke (1 , 2,0).
Jawab:
Tuliskan x(t) = t,
y(t)
= 2t, sehingga
C : r¯(t) = t¯i + 2t¯j, −1 ≤ t ≤ 1
 ds
ds √
2 = √5
= 1 + 2 dt
Jadi
1 16
Z xy3ds = Z− t(2t)3√5dt =
√
C 1 5
Kerja sebagai
integral garis
Benda bergerak dari titik A ke titik B sepanjang
lintasan
C : r¯(t) = x(t)¯i
+ y(t)¯j + z(t)k,¯ t ∈ [a,b]
oleh medan gaya
F¯(x,y,z)
= F1(x,y,z)¯i + F2(x,y,z)¯j + F3(x,y,z)k¯
Untuk menghitung kerja yang dilakukan gaya, kita perhatikan
benda pada saat di titik Q(x,y,z) seperti diilustrasikan pada
Gambar (6). 1. Vektor singgung kurva C
r¯′(t) = x′(t)¯i
+ y′(t)¯j
+ z′(t)k¯
dan vektor
singgung satuannya
, dengan |T¯| = 1
Figure
6: Sketsa medan gaya F¯ pada lintasan
C
2.
Proyeksi gaya F¯
pada T¯ w¯ = (F¯ · T¯)T¯
w¯ sebagai gaya penggerak benda, dan |w¯| = F¯ · T¯.
3.
Selama selang waktu kecil dt, benda bergerak sejauh dL.
4.
Menurut hukum fisika: kerja adalah hasil kali gaya
dengan jarak, sehingga untuk menggerakkan′ benda sejauh dL diperlukan kerja dω = (F¯ · T¯)dL.
Sedangkan dL = |r¯(t)|dt, sehingga kerja keseluruhan
Bentuk integral terakhir diperoleh setelah
menyatakan T¯ dan dL dalam r¯ seperti diberikan di atas. Dalam penulisannya kerja lebih sering
dijumpai dalam bentuk integral garis
W = Z F¯ · ds¯
C
dimana ds¯ = r¯′(t)dt.
Contoh:
Hitung kerja yang dilakukan gaya
F¯(x,y,z)
= x¯i + y¯j + zk¯
untuk menggerakkan benda sepanjang lintasan
C : r¯(t)
= sint¯i + cost¯j + tk,¯ t
∈ [0,2π]
Jawab:
Kerja W = RC F¯ · ds.¯
Untuk menghitung integral tersebut, kita harus menyatakan ke integral tentu
F¯(¯r(t)) = (sint,cost,t) ds¯ = r¯′(t)dt = (cost,−sint,1)dt
Jadi 2π
W = Z sintcost
− costsint + tdt = 2π2
0
• Bentuk diferensial dari integran Kerja yang dilakukan oleh
gaya F¯ adalah
W = Z F¯ · ds¯
C
dimana
ds¯ = r¯′(t) = dx¯i
+ dy¯j + dzk¯
Sehingga bentuk integran dapat
dituliskan dalam bentuk diferensial
F¯ · ds¯ = Z F1dx + F2dy + F3dz
C C
Hubungan
integral garis dan integral ganda
–
Tinjau R daerah
tertutup di bidang x − y yang dibatasi oleh kurva C yang dinyatakan dalam fungsi vektor
dengan orientasi positip, yaitu arah lintasan berlawan dengan perputaran jarum
jam. Daerah R dapat dinyatakan
sebagai R = {(x,y) : a ≤ x ≤ b,u(x) ≤ y
≤ v(x)}.
–
F¯(x,y) = f(x,y)¯i + g(x,y)¯j
medan vektor dengan f(x,y) dan g(x,y) kontinu pada R, begitu juga turunannya.
–
Berikut penjabaran inetgral ganda menjadi integral
garis
∂f b v
∂f
RRR ∂y dA = RR−a RRu ∂y dydx − − R −R
= ab f(x,v(x)) f(x,u(x))dx
= ba
f(x,v(x))dx ab f(x,u(x))dx = C f(x,y)dx
– Dengan
cara sama untuk R = {(x,y) : p(y) ≤ x ≤ q(y),c
≤ y ≤ d}
– Dengan
menggabungkan kedua hasil
Hubungan ini dikenal sebagai
teorema Green.
– Contoh:
Hitung I =
RC y2≤dx +−x2dy≤dengan≤ C berupa lintasan sebagai batas segiempat −1 ≤ x 1, 1 y 1 dan arah positip, yaitu berlawanan
dengan perputaran jarum jam.
Jawab:
∗ Kita hitung secara langsung
Figure 7: Lintasan C = C1
∪ C2 ∪ C3 ∪ C4 sebagai batas segi-empat R
I = Z 1 y2dx+x2dy+Z 2 y2dx+x2dy+Z 3 y2dx+x2dy+Z y2dx+x2dy
C C C C4
dengan C1,C2,C3,C4 merupakan
bagian-bagian dari lintasan C, yaitu
sebagai sisi-sisi segi-empat, seperti diberikan dalam Gambar (7).
R y2dx + x2dy = R−1 dx = 2
C 1 −1
RR 32 y2dx + x2dy = R −−11 dy
= 2− C
R y2dx + x2dy = R 1 dx = −2
C 1
4 y2dx + x2dy = R1 1 dy = 2 C
|
(dy = 0,y = − 1)
(x = 1,dx = 0)
(dy = 0,y = 1)
(x = −1,dx = 0)
|
Keseluruhan I = 0.
∗ Menggunakan teorema Green f(x,y)
= y2,g(x,y) = x2
1 1
I = Z Z 2x − 2ydA = Z− Z− 2x − 2ydxdy
= 0
R 1 1
• Integral
garis tidak bergantung lintasan
–
Dari contoh sebelum ini, kita menghitung sebagian
integral dari (-1,-1) ke (1,1) sepanjang C
= C1 ∪ C2
I = Z y2dx + x2dy
C
yang menghasilkan I = 4. Sekarang kita ambil lintasan lain, misalnya
C : r¯(t) = t¯i + t¯j, −1 ≤ t ≤ .
Substitusikan x = t,y
= t, begitu juga dx = dt,dy
= dt, integral garis menjadi
integral tentu
Di sini kita dapat membandingkan kedua integral,
dengan lintasan yang berbeda kita peroleh hasil integral yang berbeda.
–
Sekarang kita perhatikan I = RC xdx
− ydy − zdz dengan dua macam lintasan yang menghubungkan (1,0,-1) ke (2 ,
-1,0).
∗ Lintasan C : r¯(t) = (1,0,−1) + t(1,−1,1) untuk t ∈ [0,1]. Untuk
menghitung integralnya, kita substitusikan x
= 1 + t,y = −t,z = −1 + t dan dx = dt,dy
= −dt,dz = dt, sehingga diperoleh integral tentu
1 1
I =(1 + t) + t(−1) − (−1 + t)dt
= Z 2 − tdt = 3/2
0 0
∗ Lintasan C = C1
∪ C2 ∪ C3 dimana
C1 : dari (1,0,-1) ke (1 ,0,
0)
C2 : dari (1,0,0) ke (2 ,0,
0)
2
2
xdx − ydy − zdz = Z xdx = 3/2
C 1
C3 : dari (2,0,0) ke (2 ,-1, 0)
−1
3
xdx − ydy − zdz = Z −ydy = −1/2
C 0
Keseluruhan I = 3/2, diperoleh hasil
yang sama seperti pada lintasan sebelumnya.
∗ Pertanyaan:
Apakah hasil yang diperoleh di atas hanya kebetulan
sama nilainya? Jika tidak adakah syarat agar integral tidak bergantung
lintasan?
∗ Untuk lebih mendukung
pertanyaan di atas, dapat dihitung integral menggunakan lintasan lain sebagai
latihan, misalkan
C : r¯(t)
= (1 + t2)¯i − t¯j + (−1 + √t)k,¯ 0 ≤ t ≤
1.
• Turunan eksak
Definisi:
fdx + gdy + hdz dikatakan turunan eksak jika bentuk
tersebut merupakan diferensial dari fungsi skalar u(x,y,z), yaitu
Hubungan:
–
f = ∂u∂x,g = ∂u∂y,h = ∂u∂z
–
Dalam bentuk vektor
Medan vektor V¯
= f¯i + g¯j + hk¯
memberikan diferensial vektor bila
V¯ = gradu
Dari pengertian eksak, kita
dapatkan:
C fdx + gdy + hdz tidak bergantung lintasan
1.
⇔ fdx + gdy + hdz eksak
2.
⇔ Integral bernilai nol untuk setiap lintasan sederhana
tertutup pada daerah definisinya.
3.
⇔ ∂h∂y =
∂g∂z, ∂f∂z =
∂h∂x, ∂x∂g = ∂f∂y atau curlV¯ = 0.
Catatan:
Terkait dengan integral yang
bebas lintasan, terdapat ekivalensi seperti dituliskan di atas. Secara teknis,
pernyataan terakhir (ke-tiga) lebih banyak digunakan, karena untuk memeriksanya
cukup dengan menurunkan fungsi yang ada pada integran atau menggunakan curl.
• Contoh:
Tentukan− u(x,y,z) agar du = xdx
− ydy−− zdz, kemudian hitung RC xdx
− ydy zdz dengan C lintasan dari P(1,0, 1) ke Q(2,−1,0).
Jawab:
∂u = x ⇐ u(x,y,z) = x222 +
a(y,z)
∂x
∂u
= ∂a∂y = −y
⇐ a(y,z) = −2 y2 + b(z)
∂y
∂u∂z =
∂z∂b = −z ⇐ b(z)
= −z2 + K
Jadi u(x,y,z) = x22 − y22 − z22 + K.
Karena kita dapat menentukan fungsi skalar yang
diferensial-nya sama dengan xdx − ydy − zdz maka integral yang kita hadapi tidak bergantung lintasan. Oleh
karena itu
Kembali pada teorema Green, kita dapat menuliskannya
dalam bentuk vektor.
• Kaitan
dengan curl
Dari medan vektor F¯(x,y) = f(x,y)¯i + g(x,y)¯j,
kita dapat menghitung curl dari F¯
sehingga
Menurut teorema Green ruas
kanan dapat dinyatakan sebagai integral garis, sehingga diperoleh hubungan
fdx + gdy = Z Z curlF¯ · kdxdy¯
C R
atau dalam
bentuk vekto
Terimakasih Telah berkunjung di blog saya,
jika ada pertanyaan saran atau kritik bisa tulis komentar di bawahnya ^_^